By Rob Verkerk PhD, founder, executive and scientific director

You’ve just got the news from your coronavirus test centre that your test was positive. You now have to self-isolate. If you don’t, you could face a fine up to £10,000, in the UK at least.

When it comes to health, we’re all for monitoring. It’s a central plank of our blueprint for health system sustainability. But there has to be some caveats. Here are a few:

• That the test must be accurate
• If there’s a chance your test result might be wrong, you should be told
• Any actions that follow from the test result must have been subjected to a careful balancing of risk and benefit – taking into account not only health-related factors, but also social and economic ones.

On all three of these caveats, testing as rolled out in most countries – including the UK’s Test & Trace initiative – fails spectacularly.

We’re going to explain here why positive test results from RT-PCR tests are more than likely to be wrong – and why, if you’ve had a positive test result, you should make sure you’re re-tested. If compulsory self-isolation following a positive test result has a major negative impact on your work or other aspect of your life, you should think about demanding multiple re-tests.

Concerns about false positives become ever more real if you're trying to push towards millions of tests daily, as the UK government is with its Operation Moonshot. Leaked documents reveal that “new types of test [non-PCR] are likely to be less accurate [than PCR], introducing some [additional] level of risk.”, raising even greater concern, as revealed in a recent article published in one of the world's most respected medical journals, the BMJ.

>>> Share link: https://odysee.com/@ANHInternational:5/casedemic:d?r=FauvpzTPntJZUaVQsKd31Zg2Bc37UaHW

Testing for a virus not a disease

By definition, someone who’s got Covid-19 has to be diseased and present with symptoms, such as a continuous cough, shortness of breath, fever, chills, fatigue, nausea, runny nose, loss of sense of taste or smell, and so on.

But we know that the vast majority of people who’re found to be positive from a PCR test don’t have the disease. Most people have come to think of these people as asymptomatic, but the majority of these might not even be infected with SARS-CoV-2 (the virus that causes Covid-19). They therefore can’t infect others.

In our video above, we show you why it is wrong to consider positive test results as a measure of infection. Recently deceased inventor of PCR, Dr Kary Mullis, was always clear that PCR should be used for biomedical research and forensics, and not for diagnosis of disease. Echoing Mullis’ sentiments, Dr David Rasnick, biochemist and protease developer proferred, “I’m skeptical that a PCR test is ever true. It’s a great scientific research tool. It’s a horrible tool for clinical medicine.”

Accuracy, sensitivity and specificity aren’t the same

Manufacturers of PCR tests that measure whether or not you’re supposed to be infected claim values expressed as percentages for two metrics. One is sensitivity that measures the ability of the test to detect true positives, the other is specificity, which reflects the ability of the test to detect true negatives. For so-called Covid-19 RT-PCR tests, they’re often very high values close to 100%, as you’ll see in the table below:

Table: Covid-19 PCR tests – and claimed sensitivity and specificity

But these analytical values are based on tests evaluated under perfect conditions using reference samples of synthetic gene sequences. There is no proper gold standard that confirms the infection or the presence of disease, and we also know that real world accuracy of the tests varies according to the timing of the swab sample, the viral load on the specimen, and even things like whether or not someone smokes.

“A test with good analytical sensitivity and specificity does not necessarily have good clinical sensitivity and specificity. The overall performance of SARS-CoV-2 RT-PCR tests cannot be known until we understand who is truly infected and who isn’t.”
- Andrea Prinzi, American Society for Microbiology

To put it in different terms, the analytical sensitivity, under ideal lab conditions, is the proportion (percentage) of people who will have a positive result when exposed to the virus. Conversely, the specificity is the proportion that should get a negative result when there’s no disease around. When specificity for example is less than 100%, say 99%, you’d expect 1% false positives i.e. people testing positive when they should have been negative because they are not infected. A 1% error rate sounds pretty good to most people – but that 99% specificity will only give you a 99% chance of having a true negative if you’re guaranteed to be infected. That just doesn’t happen when there’s not much virus around and a lot of infected people around you.

Bayes’ re-entry

When there’s not much disease around probability theory comes into play. This general idea was first mooted posthumously by Reverend Thomas Bayes in 1763 in the form of what we know today as Bayes’ theorem or law. It took a while for medics and researchers to recognise the importance of Bayesian probability theory in clinical diagnostic and screening and Bayes’ theorem wasn’t applied to diagnostic or screening tests until the 1950s. It’s been thoroughly studied in diseases like TB.

What Bayesian probability tells us in relation to our current pandemic is that if we have information about the prior risk of infection – in other words, if we know what proportion of people in the communities we live in are infected (= disease prevalence) – we can more accurately predict the accuracy of a given test result, whether positive or negative.

High false positive rate when disease is at low ebb

Here’s the real cough drop: as the disease prevalence declines, the chances of a positive result from an RT-PCR test being a true positive declines, dramatically so at very low levels of prevalence. The converse is also true, although, fortunately, is much less relevant. When the prevalence of infection is very high, the chances that a negative test result is a true result also declines substantially.

Modelled daily rates of positive tests in different regions of the UK range from 0.04% (West Midlands) to 0.21% (North West) according to UK government stats which are themselves based on the rate of positive tests.

To understand how prevalence affects the likelihood of a test result being true, you need to calculate another statistic that includes Bayes’ theorem, the Positive Predictive Value (PPV) and the Negative Predictive Value (NPV). Here, one of the world’s greatest medical statisticians, the late Doug Altman from Oxford University needs to be credited for his application of Bayesian probability to diagnostic and screening tests.

DIY PPV

You can use many a website diagnostic calculator to compute the PPV and NPV, but remember it’s the PPV that is particularly affected by low prevalence. You can also use Altman and Bland’s 1994 formulas yourself if you want to do it the hard way, but the MedCalc is an easier option.

If you take real-world sensitivity and specificity at 95% i.e. you assume that a combination of errors in the test themselves and the way the tests perform in the real world contribute to a 5% error rate which is realistic, you get the following percentage probabilities for a positive test result being a true positive.

At 10% prevalence, PPV = 68%
At 5% = 50%
At 2% = 28%
At 1% = 16%
At 0.5% = 9%
At 0.05% = 1%

In this final scenario, which may be in line with the real world prevalence in the least infected parts of the UK, that means if you got a positive result in a test, there’s only a 1% chance it’s correct. Yes, a 1% chance.

Just tell us – we’re not stupid!

It’s not statistical trickery – it’s actually common sense. To try to understand why the false positive rate of RT-PCR tests go up when the prevalence of SARS-CoV-2 is low, let’s use the analogy of looking for a needle in a haystack; the PCR test has been designed to detect real needles. But because the test isn’t 100% accurate, especially when used in different barns and fields by different people, it sometimes picks up things that look like needles but aren’t real ones. As real needles are so few and far between, the chances of finding things that look like needles but aren’t increases. OK?

The big question we have is: WHY IS THE PUBLIC NOT BEING TOLD ABOUT THE PROBABILITY OF THEIR TEST BEING INCORRECT?

Don’t tell us the public isn’t clever enough to understand probability. The public deals with probability all the time. The probability of market prices rising or falling according to national or global events. The probability of a plane falling out of the sky when you decide to travel by air. The risk of something going seriously wrong when you consent to a given surgical procedure.

Why not now?

Could false positives explain the apparent rise in infections?

The short answer is: no. If the level of testing, test specificity and infection prevalence stays the same, it's simple: nothing changes. if the testing level goes up, the number of positive results will also go up (which is why it's so important to keep an eye on the positivity rate (the proportion of the tested population that are positive - see Fig 1 below). So what happens when the third variable, disease prevalence, changes? What happens here is that the reliability of a positive test goes down - dramatically so as we've shown above. 

In the figure below, relying on official UK government data, we present the number of tests (in Pillars 1 and 2), the number of positive tests by specimen date, and by published date, as well as the positivity rate for each method (7-day averages). The positivity rate is simply the number of positive tests as a proportion of those tested. As you will see (Fig. 1) total tests increased and this will likely account for some of the apparent increase in cases that has got everyone deeply concerned. The trouble is in the mix of the slight upward trend is a genuine rise of true positives and the effect of increased testing frequency.

You'll also notice that the way the UK Government chooses to illustrate the rise in case numbers (Fig. 2) is at odds with a more scientifically rational representation of the data, as we show in Fig. 1, which eliminates confounding by testing frequency. Unfortunately, another clear case of Government deception. As we said last week, the World Health Organization (WHO) has advised governments that before reopening economies and removing restrictions, the positivity rate should be below 5% for at least 14 days. The real positivity rate in the UK has been way below 5% for months now.

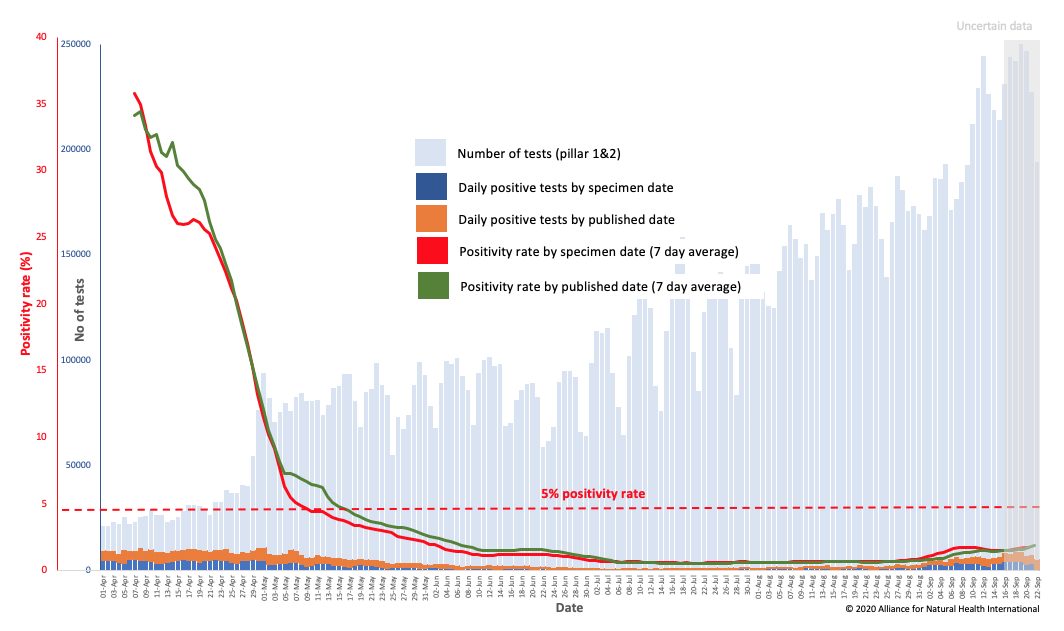
Figure 1: UK government data on number of tests, daily positive tests (by specimen and published date) and positivity rates for each (7-day averages).

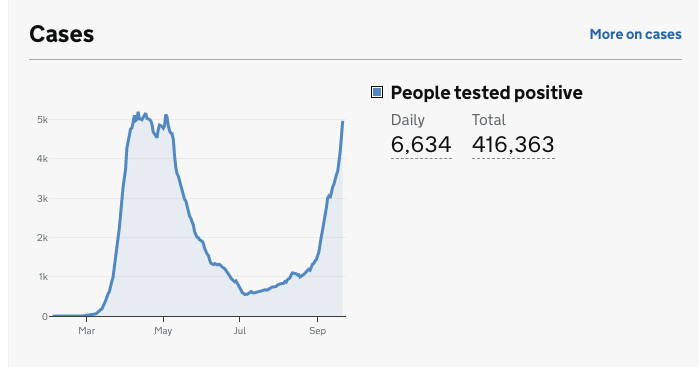
 Figure 2. The way the UK Government presents the current rise in cases. [Source: GOV.UK]

Watchful waiting and protection of the most vulnerable may have been a more proportionate response than life-changing fines for those who don’t self-isolate when they’ve been delivered a positive result for a RT-PCR test.

Especially when the chances are it was wrong.

Find out more about diagnostic tests, sensitivity, specificity and predictive values

Find out more at ANH Covid-19 Adapt Don’t Fight campaign page